The original number in table 2-1 is also called an
antilog. Notice that a number greater than one is a
positive log. Any number less than 1, but greater than
zero, is a negative log.
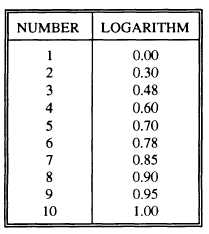
Logs are also required between the numbers 1 and
10. Since the log of 1 is 0 and the log of 10 is 1, the
numbers 1 through 9 are decimals. (See table 2-2.)
Notice the relationships between numbers and
their logs as follows:
When numbers are multiplied, their logs are
added. Example: 8 = 2
4. The sum of log 2 and
log 4 equals log 8: 0.30 + 0.60 = 0.90.
When numbers are divided, their logs are
subtracted. Example: 3 = 6
2. Log 3 is the
difference between log 6 and log 2: 0.78 - 0.30 =
0.48.
The previous discussion is provided to give you a
general idea on how logarithms are derived. It is not
necessary for you to memorize logarithms, or refer to
the log tables. All scientific calculators have a "log"
key that converts numbers to logarithmic form. You
should become familiar with the functions of your
calculator before proceeding with the study of
photographic quality assurance. For more information
on using logarithms, refer to the chapter on logarithms
in Mathematics, Volume 1, NAVEDTRA 10069.
One of the main uses of logarithms in
photographic quality assurance is to take the numbers
used to indicate exposure in characteristic curves and
reduce them to a manageable form. For example, the
sensitometer in your imaging facility is set on an
exposure time of 1/100 second and provides an
illuminance of 80,000 lux (or meter-candles). The log
exposure can be calculated easily as follows:
E T = H
80,000 (lux)
1/100 (set) = 800 lux seconds
The log exposure = the log of 800 or 2.90
When you convert exposure to logarithmic form,
both density and exposure are on the same scale. A
characteristic curve indicates how exposure and
processing differences affect photographic emulsions
by comparing density and the log of exposure.
To describe sensitometry, you must become
acquainted with several new terms and formulas. As
a starting point, you should become familiar with the
terms transmission, opacity, and density, or T, O, and
D.
TRANSMISSION
Most photographic material, even clear film, does
not transmit all of the incident light that is relevant to
it. Transmission is a measure of the light-passing
ability of a film or other medium. The transmission
of a processed film refers to the fraction, or
percentage, of incident light that passes through the
film.
In a formula, transmission is represented by a
capital letter T. The formula for determining
transmission is as follows:
Table 2-2.—Common Logarithms Between 1 and 10
T
= Amount of transmitted light
Amount of incident light
The result is never more than 1/1, or 1.00. For
example, when 10 meter-candles (mc) of light are
incident (or falling) to a film and 5 mc is passing
through it, the transmission is as follows: T = 5/10 or
T = 0.50, or 50 percent. When 2 mc is transmitted,
the formula reads T = 2/10 or 0.20, or T = 20 percent.
OPACITY
Opacity is the ability of a medium to absorb light.
The two terms, transmission and opacity, are directly
opposite in meaning. Opacity is indicated in a
2-4