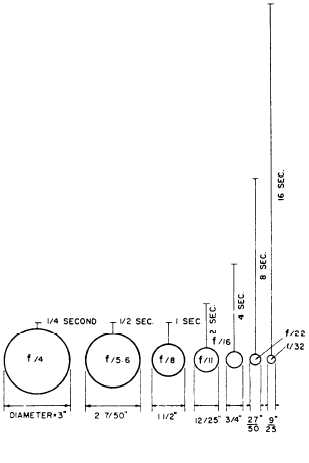
exception. All these numbers may not exactly reduce the
amount of light admitted by one half, but they are
sufficiently close for all practical purposes. However,
all of these values are in proportion to the squares of
their numbers. For example, f/4 admits four times more
light than f/8 because the square of f/4 is contained in
the square of f/8 exactly four times. Thus,
42 = 4 x 4 = 1 6
82 = 8 x 8 = 6 4
6
4
1
6= 4
Table 1-1 shows that the amount of light admitted
is inversely proportional to the square of the f/stop,
while the exposure required is directly proportional to
it.
EXAMPLE: The correct exposure at f/8 required 1
second. How long an exposure is required at f/16? The
proportion and computation are as follows:
(Old f/value)2
(Old exposure)
(New f/value)2
= (Required exposure)
82
1
1
62=x
6
4
1
=
2
5
6
x
64x = 256
x = 4
Thus the required exposure equals 4 seconds.
Table 1-1.–Comparison of f/stops with Amount of Light to Exposure Time
f/ value
f/value2 squared
Amount of light admitted
Exposure in seconds
4
1
6
4
1/4
4.5 (half stop)
20.25
3.2
1/3
5.6
31.36
2
1/2
8
64
1
1
11
121
1/2
2
16
256
1/4
4
22
448
1/16
8
32
1024
1/32
16
l-20