I
G
F= A
I =FG
A
A =FG
I
F =IA
G
G =IA
F
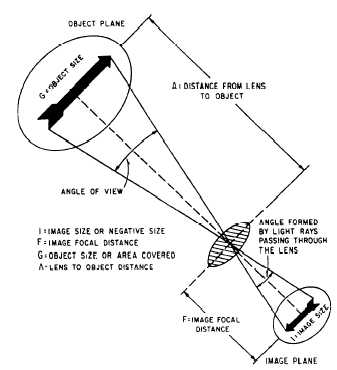
Figure 1-32.–Proportional IFGA.
All image-object and focal length distance
relationship problems can be computed with the
following simple proportion:
The image size (I)
is to the image focal distance (F)
as the object size (G)
is to the object focal distance (A)
You should thoroughly understand this equation since
you will have many uses for it in many different
applications of photography.
Study the proportional IFGA figure and note the
following:
I - the image size
F - the image focal distance
G - the object size
A - the distance from lens to object
The ratio of image size to image focal distance is
the same as the ratio of object size to object focal
distance as follows:
I:F = G:A
I =FG
A
I =
12 x 10
3
0
The mathematical equation resulting from this
proportion is as follows:
The proportion may be written in fractional form as
follows:
When solving for I:
When solving for A:
To clear or set apart one factor of an equation so it may
be solved, divide the equation by all factors on that side
of the equation except the one to be set apart.
When solving for F:
When solving for G:
These four formulas are from the same equation
IA = FG.
Inches and feet are used in the equation that
eliminates the computations required to reduce feet
measurements to inches. However, the relation of inches
to inches and feet to feet must be maintained on the
respective sides of each equation Keep I and F values
in inches and G and A values in feet. Then, when solving
for I or F, the result will be in inches. When solving for
G or A, the result will be in feet.
In the sample problems which follow, the IA = FG
formula is used as though the camera were focused at
infinity.
PROBLEM 1: A lens with a focal length of 12 inches
is used to photograph an object 10 feet high from a
distance of 30 feet. What is the size of the image? Solve
for the unknown factor (image size) by substituting the
known factors (focal length, object size, and distance)
into the equation IA = FG. The formula and
computations are as follows:
IA=FG
I = 4, or image size equals 4 inches
l-29