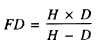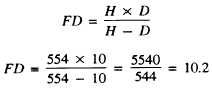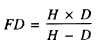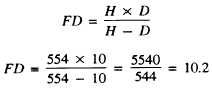ND = near distance
H = hyperfocal distance
D = distance focused upon
F D = far distance
EXAMPLE: What is the depth of field of a 155mm (6.1
inch) lens that is focused on an object 10 feet from the
camera lens using f/2.8? (Note: In a previous example
the hyperfocal distance for the lens was found to be 554
feet.) By the formula, the nearest sharp point is
determined as follows:
ND = 9.8 feet
Thus the nearest point in sharp focus is 9.8 feet from the
lens that is focused on an object at 10 feet, using f/2.8.
Also by the formula, the farthest point in sharp focus
can be determined as follows:
FD = 10.2 feet
Therefore, the far point in sharp focus is 10.2 feet when
focused on an object at 10 feet, using f/2.8.
Consequently, the depth of field in this problem equals
the near distance subtracted from the far distance
(10.2 - 9.8 = 0.4-foot depth of field). Thus all objects
between 9.8 and 10.2 feet are in acceptably sharp focus.
When this depth of field is not great enough to cover the
subject, select a smaller f/stop, find the new hyperfocal
distance, and apply the formula again.
When the only way you have to focus is by
measurement, the problem then becomes one of what
focus distance to set the lens at so depth of field is placed
most effectively. There is a formula to use to solve this
problem.
P =D x d x 2
D + d
Where:
D = distance to farthest point desired in sharp
focus
d = distance to nearest point desired in sharp
focus
p= distance to point at which the lens should be
focused
Substituting the figures from the previous examples,
D= 10.2 feet
d = 9.8 feet
P= lens focus distance
Then:
P = 10 feet
To obtain the desired depth of field at f/2.8, we set the
lens focus distance at 10 feet.
If the preceding explanations and formulas have
confused you, here is some good news! Most cameras
and lenses have depth of field indicators that show the
approximate depth of field at various distances and lens
apertures. Figure 1-30 shows that with the lens set at f/8
and focused at about 12 feet, subjects from about 9 feet
to about 20 feet are in acceptably sharp focus. By
bringing the distance focused upon to a position
opposite the index mark, you can read the depth of field
for various lens openings.
Keep in mind that a depth of field scale, either on
the camera or on the lens, is for a given lens or lens focal
length only. There is no universal depth-of-field scale
that works for all lenses.
In conclusion, the two formulas used to compute
depth of field serve for all distances less than infinity.
When the lens is focused on infinity, the hyperfocal
distance is the nearest point in sharp focus, and there is
no limit for the far point.
CONJUGATE FOCI
Object points and their corresponding image points
formed by a lens are termed conjugate focal points. The
distances from the optical center of the lens to these
points, when the image is in focus, are termed conjugate
focal distances or conjugate foci (fig. 1-31).
1-26